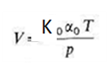 |
| Las moléculas en el estado gaseoso están constantemente chocando entre si y con las fronteras de un sistema lo que genera una presión sobre las mismas. |
De los tres estados de agregación
solo el estado gaseoso permite una descripción cuantitativa relativamente
sencilla.
En 1662, Robert Boyle realizo las
primeras medidas cuantitativas del comportamiento de los gases en relación con
la presión y el volumen. Sus resultados demostraron de el volumen es
inversamente proporcional a la presión:
V= K/P
Donde P es la presión, V el
volumen y K una constante.
Posteriores experimentos de Charles demostraron que la
constante K es una función de la temperatura. Esta es una formulación aproximada
de la ley de charles.
 |
| Volumen en función de la presión ley de Boyle |
Gay-Lussac hizo
medidas del volumen de una masa fija de gas bajo presión constante y encontró
que el volumen era una función lineal de la temperatura, esto se expresa por la
ecuación:
V= a + bt (1)
(2)
(3)
(5)
(7)
Donde t es la temperatura y a y b
son constantes. La siguiente figura muestra una grafica del volumen en función de
la temperatura.
La intersección en el eje vertical es a=V0, ósea el
volumen a 0 °C. La pendiente de la curva es la derivada
b= (∂V/∂t)p
Según esto la ecuación 1 puede escribirse en forma
equivalente:
(2)
Los experimentos de charles
demostraron que, para una masa fija de gas bajo una presión constante, el
aumento relativo de volumen por cada aumento de un grado de temperatura era el
mismo para todos los gases con los cuales el experimentó, a una presión constante
el aumento de volumen por grado es
(∂V/∂t)p por tanto el aumento
relativo de volumen por grado a 0°C es
(1/V0) (∂V/∂t)p
Esta cantidad es el coeficiente de expansión térmica a 0°C
para el cual empleamos el símbolo α0:
(3)
Según esto podemos expresar la ecuación 2 en función de α0
:
(4)
lo que es conveniente por que
expresa el volumen del gas en función del volumen a cero grados centígrados y
de una constante, α0, que es la misma para todos los gases y que además
es casi independiente de la presión a la cual se realizan las medidas. Si medimos
α0
a varias presiones encontramos que para todos los gases α0 se aproxima al mismo valor limite a P=
0. La forma de la ecuación 4 sugiere una transformación de coordenadas que debería
ser útil, es decir, define una nueva temperatura T en términos de la
temperatura original mediante la ecuación:
(5)
La ecuación 5 define
una nueva escala de temperatura llamada escala
de temperatura de gas o más
exactamente, escala de temperatura para gases ideales. La importancia de esta
escala reside en que el valor limite α0,
y por consiguiente 1/ α0 tiene
el mismo valor para todos los gases, por otra parte α0 depende
de la escala de temperatura usada originalmente para t. si t esta en grados Celsius
entonces 1/ α0 =273.15 °C, la escala T resultante es numéricamente
idéntica a la escala de temperatura termodinámica, la unidad en el SI para la
escala de temperatura termodinámica es el kelvin (K)
T = 273.15 + t
lo que convierte la ecuación 4 en:
V = V0 α0T (6)
Masa molar de un gas y ley del
gas ideal
La ley de Boyle (masa fija T constante)
y la ley de charles (masa fija P constante) se pueden combinar para formar una ecuación
general, destacando que V0 es el volumen a 0 °C y que por tanto está
relacionada con la ley de Boyle V0 =K0/P donde K0 es el
valor de la constante para t=0°C. Según esto la ecuación 5 viene a ser:
(7)
si la presión y la temperatura permanecen constantes y se duplica la masa del gas el volumen se duplica también por tanto K0 es
proporcional a la masa del gas, por consiguiente K0 =Bw donde B es
una constante y w la masa del gas, introduciendo esto tenemos
(8)
Que
es la relación general entre las cuatro variables V, w, T, y P. el valor de la
constante B es diferente para cada gas, por lo que usar este ecuación requiere
de una tabla de constantes B para todos los gases, para evitar eso expresaremos
a B en términos de una masa característica. Sea M la masa del gas en el
recipiente bajo un conjunto de condiciones estándar: T0, P0,
V0. Si se encierran diferentes gases en el volumen estándar V0 bajo las condiciones estándar de temperatura
y presión, según la ecuación 8 para cada gas tendremos
(9)
Empleando este valor de B en la ecuación 8
(8)(9)
Como las condiciones normales se
escogen a nuestra conveniencia , la relación R = P0V0/T0
tiene un valor fijo para cualquier
elección particular, y tiene por supuesto el mismo valor para todos los gases
(R se conoce como la constante de los gases), por tanto la ecuación 9 puede
escribirse como
o bien como
Sea n = w/M el entonces
PV=nRT
Esta es la ecuación de los gases ideales y es muy útil en la mayoría de los cálculos termodinámicos, sin embargo los gases reales se comportan de manera diferente en algunos momentos, por ejemplo, si enfriamos un gas real a presión constante el volumen disminuye pero llegara a una temperatura en la que empezará a licuarse y disminuirá su capacidad para comprimirse. Por otro lado a presiones altas y temperatura constante pasara lo mismo.
Ejemplo: el coeficiente de expansión térmica α está
definido por
Aplicando la ecuación de estado calcúlese el valor de α para un gas ideal.
Solución
para un gas ideal
V = nRT/P
La derivada con respecto a T manteniendo presión constante sera:
(∂V/∂T)p = nRT/P
Sustituyendo este resultado en la definición de α se encuentra que
α = (1/V) (nR/P)
y dado que de la ecuación de estado (nR/PV) = 1/T obtenemos que
α = 1/T
por lo tanto para un gas ideal α = 1/T
el siguiente vídeo ilustrara un poco las diferencias entre gases ideales y gases reales y servirá para introducción a temas mas avanzados del curso
complementos
complementos
